Stress-Dependent Porosity and Permeability of Porous Rocks Represented by a Mechanistic Elastic Cylindrical Pore-Shell Model
应力依赖性多孔岩石的孔隙率和渗透率，由机制弹性圆柱孔隙-壳模型表示

Abstract

The stress dependency of the porosity and permeability of porous rocks is described theoretically by representing the preferential flow paths in heterogeneous porous rocks by a bundle of tortuous cylindrical elastic tubes. A Lamé-type equation is applied to relate the radial displacement of the internal wall of the cylindrical elastic tubes and the porosity to the variation of the pore fluid pressure. The variation of the permeability of porous rocks by effective stress is determined by incorporating the radial displacement of the internal wall of the cylindrical elastic tubes into the Kozeny–Carman relationship. The fully analytical solutions of the mechanistic elastic pore-shell model developed by combining the Lamé and Kozeny–Carman equations are shown to lead to very accurate correlations of the stress dependency of both the porosity and the permeability of porous rocks.

1 Introduction
1 引言

This paper presents a significant progress over the previous attempts by Zhu et al. (2018) and Civan (2019a) on the application of the elastic pore-shell model. A fully analytical extension of the previous semi-analytical formulation of the stress dependency of the permeability of porous rocks by Civan (2019a) is presented. The previous formulation represents the porosity variation by effective stress using an empirical equation in the derivation of the stress-dependent permeability (see “Appendix”). The new improved mechanistic model developed in this paper expresses the stress dependency of both the porosity and the permeability of porous rocks analytically based on a cylindrical elastic pore-shell model.
本文在 Zhu 等人（2018 年）和 Civan（2019a）之前尝试应用弹性孔隙-壳模型的基础上取得了重大进展。本文提出了 Civan（2019a）之前关于孔隙岩石渗透率应力依赖性的半解析公式的完全解析扩展。之前的公式通过经验方程使用有效应力来表示孔隙率变化，在推导应力依赖性渗透率时（见“附录”）。本文中开发的新改进的力学模型基于圆柱形弹性孔隙-壳模型，从理论上表达了孔隙岩石的孔隙率和渗透率的应力依赖性。

The formulation is carried out by describing the paths of fluids flowing through heterogeneous porous rocks by a bundle of tortuous elastic capillary tubes. Then, the theoretical elastic cylindrical pore-shell model of Lamé type (Lamé 1852; Silvano 2010) is applied to express the radial displacement induced by a change in the pore fluid pressure. The variations of both the porosity and the permeability of porous rocks are determined by incorporating the radial displacement of the internal surface of the flow tubes by the variation of the pore fluid pressure into the Kozeny–Carman permeability equation (Kozeny 1927; Carman 1937a, b, 1956).
该公式通过描述流体在异质多孔岩石中流动的路径，由一束弯曲的弹性毛细管束进行计算。然后，应用 Lamé型（Lamé 1852；Silvano 2010）理论弹性圆柱孔隙-壳模型来表达孔隙流体压力变化引起的径向位移。通过将孔隙流体压力的变化引起的流动管内部表面的径向位移纳入 Kozeny-Carman 渗透率方程（Kozeny 1927；Carman 1937a，b，1956），确定了多孔岩石的孔隙率和渗透率的变化。

Critical reviews of the previous empirical and theoretical approaches for modeling of stress dependency of porosity and permeability of porous rocks have been presented in numerous publications, including Tan et al. (2015), Zhu et al. (2018), and Civan (2000, 2011, 2019b). Therefore, these reviews are not repeated here. In brief, the previous approaches mostly applied rather simple empirical constitutive equations to express the stress dependency of porosity and permeability of porous rocks in an ad hoc manner. The outstanding empirical equations proposed in the literature include the power-law (Nelson 1975), exponential-law (Wenlian et al. 2016), inverse power-law (Morrow et al. 1984), cubic-law (Gangi 1978), logarithmic-law (Bernabé 1986), and binomial-law (Seebyrger and Nur 1984; Jaeger et al. 2009).
对先前关于孔隙岩应力依赖性孔隙率和渗透率建模的实证和理论方法的批判性评论已在多篇出版物中提出，包括 Tan 等人（2015 年）、Zhu 等人（2018 年）和 Civan（2000 年、2011 年、2019 年 b）。因此，这里不再重复这些评论。简而言之，先前的方法大多应用相对简单的经验本构方程，以临时方式表达孔隙岩孔隙率和渗透率的应力依赖性。文献中提出的杰出经验方程包括幂律（Nelson 1975 年）、指数律（Wenlian 等人 2016 年）、逆幂律（Morrow 等人 1984 年）、立方律（Gangi 1978 年）、对数律（Bernabé 1986 年）和二项式律（Seebyrger 和 Nur 1984 年；Jaeger 等人 2009 年）。

The theoretical models are generally very complex. Amongst the important theoretical models are the cylindrical and spherical pore deformation models (Gangi 1978; Yale 1984; Tan et al. 2015), elastic–plastic material model (Morris et al. 2003), viscoelastic rheological models employing the Maxwell elements of mass, springs, and dashports (Yarushina et al. 2013; Yarushina and Podladchinov 2014), the pore-shell model (Ghabezloo et al. 2009), a semi-analytic equation resulting from the elastic pore-shell model (Civan 2019a) and a modified power-law equation resulting from a kinetic model (Civan 2019b).
理论模型通常非常复杂。其中重要的理论模型包括圆柱形和球形孔隙变形模型（Gangi 1978；Yale 1984；Tan 等 2015）、弹塑性材料模型（Morris 等 2003）、采用质量、弹簧和阻尼器的粘弹性流变模型（Yarushina 等 2013；Yarushina 和 Podladchinov 2014）、孔隙-壳模型（Ghabezloo 等 2009）、由弹性孔隙-壳模型得出的半解析方程（Civan 2019a）以及由动力学模型得出的改进幂律方程（Civan 2019b）。

The semi-analytical solution derived previously by combining the Lamé and Kozeny–Carman equations and applying a linear empirical equation of stress-dependent porosity was shown to yield accurate correlations of the stress dependency of the permeability of porous rocks (Civan 2019a). However, this derivation was only semi-analytical because the derivation was accomplished by incorporating an empirical exponential decay equation of stress dependence of porosity approximated further by a linear truncated Taylor series expansion following Zhu et al. (2018) (see “Appendix”). As a result, only the permeability but not the porosity of porous rocks has been formulated theoretically in the previous formulation.
之前通过结合 Lamé方程和 Kozeny-Carman 方程，并应用一个线性经验应力相关孔隙率方程得到的半解析解，已被证明可以准确关联孔隙岩石渗透率的应力依赖性（Civan 2019a）。然而，这种推导仅是半解析的，因为推导是通过结合孔隙率应力依赖性的经验指数衰减方程，并进一步通过 Zhu 等人（2018）的线性截断泰勒级数展开来完成的（见“附录”）。因此，在先前的公式中，只有孔隙岩石的渗透率而不是孔隙率被理论化地表达。

In the present paper, this limitation of the previous formulation is circumvented successfully by deriving the equations of stress dependence of both the porosity and the permeability of porous rocks by a fully analytical mechanistic model without resorting to any empirical equations. Consequently, the fully analytical relationships derived in this paper can express the effective stress dependency of both the porosity and the permeability of porous rocks in rather convenient forms which are suitable for practical applications. This formulation is based on a Lamé-type equation (Lamé 1852; Silvano 2010) expressing the change of pore size by effective stress and therefore porosity, and the Kozeny–Carman equation expressing the change of permeability by effective stress (Kozeny 1927; Carman 1937a, b, 1956).
在本文中，通过推导出多孔岩石孔隙率和渗透率应力依赖性的完全解析机制模型方程，成功克服了先前公式的局限性，而没有求助于任何经验公式。因此，本文推导出的完全解析关系可以以相当方便的形式表达多孔岩石孔隙率和渗透率的有效应力依赖性，这些形式适合实际应用。该公式基于 Lamé型方程（Lamé 1852；Silvano 2010），该方程表示有效应力对孔隙尺寸（因此是孔隙率）的变化，以及 Kozeny–Carman 方程表示有效应力对渗透率的变化（Kozeny 1927；Carman 1937a, b, 1956）。

The accuracy of the present fully theoretical formulations is validated by the analyses and correlations of the stress-dependent porosity data of Jones et al. (2001) of the coarsening-upwards (CU2) units of the North Sea reservoir and the stress-dependent permeability data of Zhu et al. (2018) for the tight sandstone samples gathered from the upper Paleozoic Shanxi and Xiashihezi formations of the South Ordos basin, China.
本文所提出的完全理论公式的准确性通过 Jones 等人（2001 年）对北海储层向上粗化（CU2）单元的应力相关孔隙率数据的分析和相关性以及 Zhu 等人（2018 年）对中国鄂尔多斯盆地南缘上古生界山西组和西夏河组致密砂岩样品的应力相关渗透率数据的分析得到了验证。

The conventional bundle of tubes model applied in this paper yields very accurate correlations of the experimental data with the coefficients of regressions equal or very close to R² = 1.0. However, in view of the complicated pore structure of the solid matrix of heterogeneous and anisotropic porous reservoir rocks, investigation of some improvements by modifications of the classical Kozeny–Carman equation is recommended in future studies to account for the contributions of micro-channels with different spatial orientations (Abdalrahman et al. 2015) and the possibility of cross-flow between the bundle of leaky tubes (Civan 2001, 2002, 2017).
本文采用的常规管束模型在实验数据与回归系数等于或非常接近 R² = 1.0 的情况下，对实验数据进行了非常准确的关联。然而，鉴于异质各向异性多孔储层固体基质复杂的孔隙结构，建议在未来的研究中通过修改经典的 Kozeny-Carman 方程进行一些改进，以考虑不同空间取向的微通道的贡献以及泄漏管束之间交叉流的可能性（Abdalrahman 等人，2015 年；Civan，2001 年，2002 年，2017 年）。

2 Mechanistic Modeling of Stress-Dependent Porosity and Permeability of Porous Rocks
2 机制建模孔隙岩石的应力依赖性孔隙率和渗透率

A fully theoretical formulation of the effective stress dependency of both the porosity and the permeability of porous rocks is developed in this section by the applications of a mechanistic cylindrical elastic pore-shell model (Lamé 1852; Silvano 2010) and the Kozeny–Carman equation (Kozeny 1927; Carman 1937a, b, 1956).
本节通过应用力学圆柱弹性孔壳模型（Lamé 1852；Silvano 2010）和 Kozeny–Carman 方程（Kozeny 1927；Carman 1937a, b, 1956），对多孔岩石的孔隙率和渗透率的有效应力依赖性进行了完全理论上的阐述。

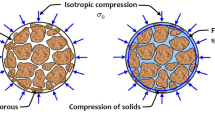
The preferential flow paths formed during flow of fluids through heterogeneous porous rocks are represented by a bundle of tortuous cylindrical elastic capillary tubes with an average internal radius r₁. The internal radius r₁ of the elastic tubes varies when the pressure p₁ of the pore fluid flowing through the tubes varies. An average external radius r₂ of the flow tubes is visualized as a fixed prescribed location beyond which the porous matrix deformation does not happen. It represents the range of influence of the pore fluid pressure effect.
在流体通过异质多孔岩石流动过程中形成的优先流动路径，由一束平均内部半径为 r ₁ 的曲折圆柱弹性毛细管束表示。当通过管子的孔隙流体压力 p ₁ 变化时，弹性管的内部半径 r ₁ 会发生变化。流动管的平均外部半径 r ₂ 被描绘为固定预定位置，在此位置之外，多孔基质变形不会发生。它代表了孔隙流体压力效应的影响范围。

In the following formulation, n represents the number of flow tubes formed in porous rock in the flow direction, L₁ and L_b the average length of the tortuous flow tubes and the bulk length of porous rock, $\tau$ the average tortuosity of the flow tubes, and A₁ and A_b the total cross-sectional areas of the flow tubes and the bulk of porous rock normal to flow direction, respectively.
在以下公式中，表示在孔隙岩石中流动方向上形成的流动管数量，以及曲折流动管的平均长度和孔隙岩石的总体积长度， $\tau$ 表示流动管的平均曲折度，以及流动管和孔隙岩石总体积垂直于流动方向的总横截面积，分别表示为和。

Consider the following founding equations of the Kozeny–Carman relationship of permeability (Kozeny 1927; Carman 1937a, b, 1956). The porosity $\varphi$ of porous rock is given by:
考虑以下渗透率 Kozeny-Carman 关系的奠基方程（Kozeny；Carman，）。多孔岩石的孔隙率 $\varphi$ 由以下公式给出：

$$\varphi =\frac{V_1}{V_{\text{b}}}=\frac{n{A}_1{L}_1}{A_{\text{b}}{L}_{\text{b}}}=\frac{n\pi r_1^2\tau }{A_{\text{b}}}$$

(1)

where V₁ and V_b are the pore and bulk volumes of porous rock, respectively.
其中 V ₁ 和 V _b 分别为孔隙岩石的孔隙体积和总体积。

Let a new variable f be defined as:
定义一个新的变量 f 为：

$$f=\sqrt{\varphi }$$

(2)

Applying Eq. (2) to Eq. (1) yields:
将公式（2）应用于公式（1）得到：

$$r_1=\sqrt{\frac{A_{\text{b}}\varphi }{n\pi \tau }}=\sqrt{\frac{A_{\text{b}}}{n\pi \tau }}f=\alpha f,\text{where }\tau =\frac{L_1}{L_{\text{b}}},\alpha =\sqrt{\frac{A_{\text{b}}}{n\pi \tau }}$$

(3)

The volumetric flow rate q of the fluid flowing through porous media and the bundle of flow tubes are expressed by:
流体通过多孔介质和流管束的体积流量 q 表达为：

$$q=\frac{K{A}_{\text{b}}}{\mu }\frac{\mathrm{\Delta }p}{L_{\text{b}}}=n\frac{\pi r_1^4}{8\mu }\frac{\mathrm{\Delta }p}{L_1}$$

(4)

where p = p₁ at the internal radius r₁ is the pore fluid pressure and $\mu$ the pore fluid viscosity. Thus, the intrinsic permeability K of porous rock is determined by applying Eqs. (3) and (4) as:
在内部半径 r ₁ 处，p = p ₁ 为孔隙流体压力，\( \mu \) 为孔隙流体粘度。因此，多孔岩石的本征渗透率 K 通过应用公式（3）和（4）确定，如下所示：

$$K=\frac{n\pi r_1^4}{8A_{\text{b}}\tau }=\frac{n\pi {\alpha }^4{f}^4}{8A_{\text{b}}\tau }=\frac{n\pi f^4}{8A_{\text{b}}\tau }{\left(\frac{A_{\text{b}}}{n\pi \tau }\right)}^2=\frac{f^4}{8{\tau }^3}\left(\frac{A_{\text{b}}}{n\pi }\right)$$

(5)

Next, define another variable gas:
接下来，定义另一个变量气体：

$$g=K^{1/\phantom{14}4}$$

(6)

Thus, combining Eqs. (5) and (6) yields:
因此，结合公式（5）和（6）得到：

$$f={\left(\frac{8{\tau }^{3}n\pi }{A_{\text{b}}}\right)}^{1/\phantom{14}4}{K}^{1/\phantom{14}4}=\beta K^{1/\phantom{14}4}=\beta g\text{where,}\beta ={\left(\frac{8{\tau }^{3}n\pi }{A_{\text{b}}}\right)}^{1/\phantom{14}4}$$

(7)

The initial porosity ${\varphi }_{\text{o}}$, permeability K_o, and internal radius r_o of the bundle of flow tubes of porous rock under the initial pore fluid pressure p_o inside the flow tubes and effective stress ${\text{σ}}_{\text{o}}$ are specified as the initial conditions, respectively, by:
初始孔隙率 ，渗透率，以及多孔岩石中流动管束的内部半径在流动管内的初始孔隙流体压力和有效应力 下分别作为初始条件，由以下方式指定：

$$\varphi ={\varphi }_{\text{o}},K=K_{\text{o}},r_1=r_{\text{o}}\text{ at }{p}_1=p_{\text{o}},\text{σ}={\text{σ}}_{\text{o}}$$

(8)

The amended Biot’s (1941) law defines the net confining pressure or effective stress $\text{σ}$ acting upon porous rocks as the total confining stress ${\text{σ}}_{\text{c}}$ minus a partial contribution of the pore fluid pressure p (Biot and Willis 1957; Zimmerman 1991; Byerlee and Zoback 1975; Zoback and Byerlee 1975):
修正的 Biot 定律定义作用于多孔岩石上的净围压或有效应力 为总围压 减去孔隙流体压力的部分贡献（Biot 和 Willis；Zimmerman；Byerlee 和 Zoback；Zoback 和 Byerlee）：

$$\text{σ}={\text{σ}}_{\text{c}}-\mathrm{X}p$$

(9)

where $\mathrm{X}$ is called the Biot–Willis poroelastic coefficient. When the confining stress remains constant, the effective stress can be related to the pore fluid pressure by applying Eqs. (8) and (9):
其中称为比奥-威利斯孔隙弹性系数。当围压保持不变时，可以通过应用等式 () 和 () 将有效应力与孔隙流体压力联系起来：

$$\text{σ}=p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}-p\mathrm{X}$$

(10)

The radial displacement ${\delta }_{\text{r}}$ at any radius r which occurs because of the pressures p₁ and p₂ applied over the internal surface at radius r₁ and the external surface at radius r₂ of a cylindrical elastic flow tube can be determined by a Lamé-type equation, given as (Lamé 1852; Silvano 2010):
在任何半径处，由于内部表面半径和外部表面半径的压力以及施加在圆柱弹性流动管上的压力引起的径向位移可以通过 Lamé型方程确定，该方程如下（Lamé；Silvano）：

$${\delta }_{\text{r}}=\left(\frac{1-\upsilon }{E}\right)\left(\frac{r_1^2{p}_1-r_2^2{p}_2}{r_2^2-r_1^2}\right)r+\left(\frac{1+\upsilon }{E}\right)\left[\frac{r_1^2{r}_2^2\left(p_1-p_2\right)}{r_2^2-r_1^2}\right]\frac{1}{r}$$

(11)

where E denotes the Young’s modulus and $\upsilon$ the Poisson’s ration of the tube material.
其中 E 表示管材的杨氏模量，υ表示管材的泊松比。

Whereas only the internal radius of the flow tubes is reduced by expansion of porous matrix from an initial radius r_o to a radius r₁ upon reduction in the pore fluid pressure p₁ inside the flow tubes from the initial pressure p_o to a pressure p₁. But, the pressure p₂ at r₂ remains constant based on the definition of the external radius r₂ taken as a fixed outer radius of the flow tubes beyond which no deformation occurs. Thus, the radial displacement ${\delta }_{r_1}$ of the internal surface radius r₁ which occurs because of the pressure p₁ applied at the internal radius r₁ is given by the following simplified form of Eq. (11) (Silvano 2010):
而当多孔介质从初始半径扩张到半径时，只有流动管的内部半径会减小。但是，根据将外部半径定义为流动管固定外半径且在此半径之外不发生变形的定义，压力保持不变。因此，由于在内部半径施加压力而发生的内部表面半径的径向位移 ，可以用以下简化的方程式（Silvano）表示：

$${\delta }_{r_1}=r_0-r_1=\left(\frac{1-\upsilon }{E}\right)\left(\frac{r_1^2{p}_1}{r_2^2-r_1^2}\right)r_1+\left(\frac{1+\upsilon }{E}\right)\left(\frac{r_1^2{r}_2^2{p}_1}{r_2^2-r_1^2}\right)\frac{1}{r_1}$$

(12)

Solving Eq. (12) for the pore fluid pressure p = p₁ inside the flow tubes gives:
解方程（12）得到流动管内孔隙流体压力 p = p ₁ ：

$$p\equiv p_1=\frac{r_0{r}_2^2-r_0{r}_1^2-r_1{r}_2^2+r_1^3}{\left(\frac{1-\upsilon }{E}\right)r_1^3+\left(\frac{1+\upsilon }{E}\right)r_2^2{r}_1}$$

(13)

Then, substituting Eq. (13) for p = p₁ in Eq. (10) yields:
然后，将方程（13）中的 p = p ₁ 代入方程（10）中，得到：

$$\text{σ}=p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}-\frac{E\mathrm{X}}{1-\upsilon }\left[\frac{r_0{r}_2^2-r_0{r}_1^2-r_1{r}_2^2+r_1^3}{r_1^3+\left(\frac{1+\upsilon }{1-\upsilon }\right)r_2^2{r}_1}\right]$$

(14)

Substituting Eq. (3) for r₁ in Eq. (14) and then rearranging yield the following expression that can be used to correlate between porosity $\varphi$ and effective stress $\text{σ}$ in an implicit manner as demonstrated in the next section:
将公式()代入公式()中，然后重新排列，可以得到以下表达式，该表达式可以隐式地关联孔隙率 和有效应力 ，如下一节所示：

$$\text{σ}\left(f^3+ef\right)=a{f}^3+b{f}^2+cf+d=Y,\text{ where }f=\sqrt{\varphi }$$

(15)

where the various parameters are defined by:
其中，各种参数由以下定义：

$$\begin{array}{rl}& a=p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}-\left(\frac{E\mathrm{X}}{1-\upsilon }\right),b=\left(\frac{E\mathrm{X}}{1-\upsilon }\right)\frac{r_0}{\alpha },c=\left[\left(p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}\right)\left(\frac{1+\upsilon }{1-\upsilon }\right)+\left(\frac{E\mathrm{X}}{1-\upsilon }\right)\right]\frac{r_2^2}{{\alpha }^2},\\ & d=-\left(\frac{E\mathrm{X}}{1-\upsilon }\right)\frac{r_0{r}_2^2}{{\alpha }^3},\text{and}e=\left(\frac{1+\upsilon }{1-\upsilon }\right)\frac{r_2^2}{{\alpha }^2}\end{array}$$

(16)

The unknown coefficients a, b, c and d of the third-order polynomial of Eq. (15) are determined by best fit of data resulting in the maximum value for the coefficient of regression R² by adjusting the value of e. Then, the relationships given by Eq. (16), which express the new parameters in terms of the actual physical parameters, are applied to determine the values of the actual physical parameters (the Biot–Willis poroelastic coefficient $\mathrm{X}$, the Young’s modulus E, the Poisson’s ration $\upsilon$, and the average external radius r₂ of the flow tubes).
第三阶多项式方程()中的未知系数、和由数据最佳拟合确定，以使回归系数的最大值对应于的调整值。然后，通过将新参数表示为实际物理参数的关系式（），应用给定的关系式，以确定实际物理参数的值（Biot-Willis 多孔弹性系数 ，杨氏模量，泊松比 ，以及流动管的平均外部半径）。

In view of the above derivation of the rigorous Eq. (15), there is absolutely no need to approximate the stress dependency of porosity by an empirical equation according to Zhu et al. (2018) and Civan (2019a) as described in “Appendix.”
鉴于上述严格的方程(15)的推导，根据 Zhu 等人（2018）和 Civan（2019a）的描述，在“附录”中，没有必要根据经验方程近似孔隙率的应力依赖性。

Finally, substituting Eq. (7) into Eq. (15) yields the following expression that can be used to correlate between permeability and effective stress in an implicit manner as demonstrated in the following section:
最后，将方程(7)代入方程(15)，得到以下表达式，可以隐式地关联渗透率和有效应力，如下节所示：

$$\text{σ}\left(g^3+Fg\right)=A{g}^3+B{g}^2+Cg+D=Z,\text{ where }g=K^{1/\phantom{14}4}$$

(17)

where the various new parameters are defined by:
各个新参数的定义如下：

$$A=a,B=\frac{b}{\beta },C=\frac{c}{{\beta }^2},D=\frac{d}{{\beta }^3},F=\frac{e}{{\beta }^2}$$

(18)

The unknown coefficients A, B, C and D of the third-order polynomial of Eq. (17) are determined for the best fit of data yielding a maximum value in the coefficient of regression R² by adjusting the value of F. Then, the relationships given by Eqs. (15) and (18) expressing the new parameters in terms of the actual physical parameters as defined above can be utilized to determine the values of the actual physical parameters (the Biot–Willis poroelastic coefficient $\mathrm{X}$, the Young’s modulus E, the Poisson’s ration $\upsilon$, and the average external radius r₂ of the flow tubes).
通过调整值，确定方程()中三次多项式的未知系数，以获得最大回归系数，从而实现数据的最佳拟合。然后，可以利用表示新参数与上述定义的实际物理参数之间关系的方程()和()，来确定实际物理参数的值（Biot-Willis 孔隙弹性系数 ，杨氏模量，泊松比 ，以及流动管的平均外部半径）。

The accuracy of the present fully theoretical formulations is validated by various examples presented in the following two sections by correlating the stress-dependent porosity data of Jones et al. (2001) of the coarsening-upwards (CU2) units of the North Sea reservoir and the stress-dependent permeability data of Zhu et al. (2018) for eight tight sandstone core samples extracted from the upper Paleozoic Shanxi and Xiashihezi formations of the South Ordos basin, China.
本文中完全理论公式的准确性通过以下两节中给出的各种示例进行验证，这些示例通过将 Jones 等人（2001 年）关于北海储层向上粗化（CU2）单元的应力相关孔隙率数据与 Zhu 等人（2018 年）关于从中国鄂尔多斯盆地上古生界山西组和西夏河子组提取的八个致密砂岩岩心样品的应力相关渗透率数据进行相关性分析。

3 Correlation of Stress-Dependent Porosity
3 应力相关孔隙率的关联

The data of Jones et al. (2001) on the stress-dependent porosity of the coarsening-upwards (CU2) units of the North Sea reservoir are analyzed and correlated here. The core samples were uploaded at an initial effective stress value of 2.8 MPa. Then, the laboratory tests were conducted by increasing the confining stress up to a maximum of 34.5 MPa. The correlation plots are presented here only for the CU2 core data using Eq. (15) above the critical effective stress of 9 MPa because of space limitation. The critical effective stress was defined as the effective stress above which the natural or induced fractures of porous rocks are closed (Civan 2019b).
本文分析了 Jones 等人（2001 年）关于北海储层向上粗化（CU2）单元的应力相关孔隙率数据。岩心样品在初始有效应力值为 2.8 MPa 时上传。然后，通过增加围压至最大 34.5 MPa 进行实验室测试。由于空间限制，此处仅展示了使用上述公式（15）在临界有效应力 9 MPa 以上的 CU2 岩心数据的相关图。临界有效应力定义为孔隙岩石的自然或诱导裂缝关闭时的有效应力（Civan 2019b）。

Figure 1 shows the CU2 core loading porosity versus effective stress data of Jones et al. (2001). Figure 2 shows the correlation of the CU2 core loading porosity versus effective stress data of Jones et al. (2001) using the present theoretical pore-shell model. Figure 3 shows a comparison of the correlation versus measured CU2 core loading effective stress data of Jones et al. (2001). Figure 4 shows the correlation of the measured CU2 core loading porosity data of Jones et al. (2001) versus the correlation effective stress. Figure 5 shows the accurate comparison of the correlation versus measured CU2 core loading porosity data of Jones et al. (2001). The correlation of the experimental data is very accurate with the coefficient of regression equal to R² = 1.0. Table 1 presents the correlations and the coefficients of correlations of the loading porosity data of Jones et al. (2001) using present theoretical pore-shell model developed here.
图 1 显示了 Jones 等人（2001 年）的 CU2 核心加载孔隙度与有效应力数据。图 2 显示了使用当前理论孔隙-壳模型对 Jones 等人（2001 年）的 CU2 核心加载孔隙度与有效应力数据的关联。图 3 显示了关联与 Jones 等人（2001 年）测量的 CU2 核心加载有效应力数据的比较。图 4 显示了 Jones 等人（2001 年）测量的 CU2 核心加载孔隙度数据与关联有效应力的关联。图 5 显示了关联与 Jones 等人（2001 年）测量的 CU2 核心加载孔隙度数据的准确比较。实验数据的关联非常准确，回归系数等于 R ² = 1.0。表 1 展示了使用在此开发的当前理论孔隙-壳模型对 Jones 等人（2001 年）的加载孔隙度数据的关联及其相关系数。

Fig. 1
图 1

The CU2 core loading porosity versus effective stress data of Jones et al. (2001)
琼斯等人（2001 年）的 CU2 核心加载孔隙度与有效应力数据

Fig. 2
图 2

Correlation of the CU2 core loading porosity versus effective stress data of Jones et al. (2001) using the present theoretical pore-shell model
铜核加载孔隙度与 Jones 等人（2001）的有效应力数据的关联，使用当前的理论孔隙-壳模型

Fig. 3
图 3

Comparison of the correlation versus measured CU2 core loading effective stress data of Jones et al. (2001)
比较 Jones 等人（2001 年）的 CU2 核心加载有效应力数据与相关性的比较

Fig. 4
图 4

Correlation of the measured CU2 core loading porosity data of Jones et al. (2001) versus the correlation effective stress
测量数据中 Jones 等人（2001 年）的 CU2 核心加载孔隙率与有效应力相关性的相关性

Fig. 5
图 5

Comparison of the correlation versus measured CU2 core loading porosity data of Jones et al. (2001) above 9 MPa
Jones 等人（2001 年）在 9 MPa 以上比较相关性与测量的 CU2 岩心加载孔隙度数据

Table 1 Correlations and the coefficients of correlations of the CU2 core loading porosity data of Jones et al. (2001) using present theoretical pore-shell model developed here
表 1 Jones 等人（2001 年）的 CU2 核心加载孔隙度数据与本文开发的孔隙壳模型的相关性及相关系数

4 Correlation of Stress-Dependent Permeability
4 应力依赖性渗透率的相关性

The data of Zhu et al. (2018) on the stress-dependent permeability of eight tight sandstone core samples of the upper Paleozoic Shanxi and Xiashihezi formations of the South Ordos basin, China, are analyzed here and compared with the previous results obtained by Zhu et al. (2018) and subsequently by Civan (2019a). The laboratory tests were conducted under a constant ${\text{σ}}_c$ = 40 MPa confining stress by reducing the pore fluid pressure p from the initial p_o = 20 MPa to the final p_final = 1.5 MPa.
本文分析了朱等人（ ）关于中国鄂尔多斯盆地南缘上古生界山西组和西夏河子组八块致密砂岩岩心样品应力依赖性渗透率的数据，并将其与朱等人（ ）和随后的 Civan（a）获得的结果进行了比较。实验室测试在 40 MPa 的恒定围压下进行，通过将孔隙流体压力从初始的 20 MPa 降低到最终的 1.5 MPa。

Figure 6 shows the loading permeability versus effective stress data of Zhu et al. (2018) for various cores. However, the correlation plots only for the Erdos-4-7 core data using Eq. (17) are presented here because of space limitation. Figure 7 shows the correlation of the Erdos-4-7 core loading permeability versus effective stress data of Zhu et al. (2018) using the present theoretical pore-shell model. Figure 8 shows a comparison of the correlation versus measured Erdos-4-7 core loading effective stress data of Zhu et al. (2018). Figure 9 shows the correlation of the measured Erdos-4-7 core loading permeability data of Zhu et al. (2018) versus the correlation effective stress. Figure 10 shows the comparison of the correlation versus Erdos-4-7 core permeability data of Zhu et al. (2018).
图 6 显示了 Zhu 等人（2018）对各种岩心的加载渗透率与有效应力数据。然而，由于空间限制，这里只展示了使用公式（17）对 Erdos-4-7 岩心数据的相关性图。图 7 显示了使用当前理论孔隙-壳模型计算出的 Zhu 等人（2018）的 Erdos-4-7 岩心加载渗透率与有效应力数据的相关性。图 8 显示了 Zhu 等人（2018）的 Erdos-4-7 岩心加载有效应力测量数据与相关性数据的比较。图 9 显示了 Zhu 等人（2018）的 Erdos-4-7 岩心加载渗透率测量数据与相关性有效应力的相关性。图 10 显示了 Zhu 等人（2018）的 Erdos-4-7 岩心渗透率数据与相关性数据的比较。

Fig. 6
图 6

Loading permeability versus effective stress data of Zhu et al. (2018)
珠等（2018）的渗透率与有效应力数据

Fig. 7
图 7

Correlation of the Erdos-4-7 core loading permeability versus effective stress data of Zhu et al. (2018) using the present theoretical pore-shell model
使用当前理论孔隙-壳模型，将 Zhu 等人（2018）的 Erdos-4-7 核心加载渗透率与有效应力数据的相关性进行比较

Fig. 8
图 8

Comparison of the correlation versus measured Erdos-4-7 core loading effective stress data of Zhu et al. (2018)
珠等（2018）的 Erdos-4-7 核心加载有效应力数据的相关性与测量值的比较

Fig. 9
图 9

Correlation of the measured Erdos-4-7 core loading permeability data of Zhu et al. (2018) versus the correlation effective stress
测量 Zhu 等人（2018 年）的 Erdos-4-7 核心加载渗透率数据与相关有效应力的相关性

Fig. 10
图 10

Comparison of the correlation versus Erdos-4-7 core permeability data of Zhu et al. (2018)
比较 Zhu 等人（2018 年）的 Erdos-4-7 核心渗透率数据与相关性的对比

Table 2 shows the correlations and the coefficients of correlations for the permeability data of Zhu et al. (2018) obtained here for the eight core samples. Figure 11 shows the comparison of the correlation permeability obtained by the present theoretical pore-shell model with the measured permeability data of Zhu et al. (2018) for all core samples. Table 3 also shows the coefficients of correlations of the permeability data obtained by Zhu et al. (2018) for the eight core samples using different models. Table 4 shows the ranking of the available models based on the average coefficients of correlations. As can be seen, the present and the previous cylindrical elastic pore shale models yield practically the same results of very high quality. These correlations of the experimental data are very accurate with the coefficients of regressions equal or very close to R² = 1.0. However, the semi-analytical equation of Zhu et al. (2018) produced lower quality results because of the errors involved in their formulation as pointed out earlier by Civan (2019a).
表 2 展示了在此获得的八个核心样品的渗透率数据的相关性和相关系数。图 11 展示了当前理论孔隙-壳模型获得的渗透率相关性与 Zhu 等人（2018 年）对所有核心样品测量的渗透率数据的对比。表 3 还展示了 Zhu 等人（2018 年）使用不同模型获得的八个核心样品的渗透率相关系数。表 4 展示了基于平均相关系数的可用模型的排名。如图所示，当前和先前的圆柱形弹性孔隙页岩模型产生了几乎相同的高质量结果。这些实验数据的相关性非常准确，回归系数等于或非常接近 R ² = 1.0。然而，Zhu 等人（2018 年）的半解析方程由于之前 Civan（2019a）指出的公式中的误差，产生了较低质量的结果。

Table 2 Correlations and the coefficients of correlations of the loading permeability data of Zhu et al. (2018) using present theoretical pore-shell model developed here
表 2 使用此处开发的机制性弹性圆柱孔壳模型对朱等人（2018 年）的加载渗透率数据的相关性和相关系数

Fig. 11
图 11

Comparison of the correlation permeability obtained by the present theoretical pore-shell model with the measured permeability data of Zhu et al. (2018) for all core samples
比较当前理论孔隙-壳模型获得的关联渗透率与 Zhu 等人（2018 年）对所有岩心样品测量的渗透率数据的相关性

Table 3 Correlations and the coefficients of correlations of the loading permeability data of Zhu et al. (2018) using present theoretical pore-shell model developed here
表 3 使用本文开发的机制性弹性圆柱孔壳模型对 Zhu 等人（2018 年）的加载渗透率数据的相关性和相关系数

Table 4 Coefficients of correlations of the loading permeability data of Zhu et al. (2018) using different models
表 4 使用不同模型对 Zhu 等人（2018 年）的加载渗透率数据的相关系数

5 Discussion and Conclusions
5 讨论与结论

This paper presented an improved and rigorous application of a cylindrical elastic pore-shell model. An effective mechanistic modeling and correlation of the stress dependency of both the porosity and the permeability of porous rocks has been accomplished without resorting to any empirical equations. The present formulations provide valuable insights into the mechanism and physics of the stress dependence of both the porosity and the permeability of porous rocks based on a Lamé-type equation of a bundle of elastic capillary tubes model (Lamé 1852; Silvano 2010) and the Kozeny–Carman relationship of permeability (Kozeny 1927; Carman 1937a, b, 1956).
本文提出了一种改进且严格的圆柱弹性孔壳模型的应用。在不依赖任何经验方程的情况下，实现了对多孔岩石孔隙率和渗透率应力依赖性的有效机制建模和相关性。本文的公式基于弹性毛细管束模型的 Lamé型方程（Lamé 1852；Silvano 2010）和多孔率渗透率的 Kozeny-Carman 关系（Kozeny 1927；Carman 1937a, b, 1956），为多孔岩石孔隙率和渗透率应力依赖性的机制和物理提供了有价值的见解。

The fully analytical equations derived by this approach for porosity and permeability resulted in accurate correlations of the stress dependency of the porosity data of Jones et al. (2001) and the stress dependency of the permeability data of Zhu et al. (2018) and ranked much better than the equation of Zhu et al. (2018). The present and the previous (Civan 2019a) cylindrical elastic pore shale models yield practically the same quality and very accurate results in the correlations of the experimental data with the coefficients of regressions equal or very close to R² = 1.0. However, the results obtained by Zhu et al. (2018) produce low-quality results because of the errors involved in their formulation as pointed out by Civan (2019a).
该方法推导出的孔隙率和渗透率完全解析方程，对 Jones 等人（2001 年）孔隙率数据的应力依赖性和 Zhu 等人（2018 年）渗透率数据的应力依赖性进行了准确的关联，其结果优于 Zhu 等人（2018 年）的方程。本方法和之前的（Civan 2019a）圆柱形弹性孔隙页岩模型在将实验数据与回归系数相关联时，实际上产生了相同的质量和非常准确的结果，回归系数等于或非常接近 R ² = 1.0。然而，由于 Civan（2019a）指出的其公式中的错误，Zhu 等人（2018 年）得到的结果质量较低。

The mechanistic model and the resulting equations developed in this paper for the porosity and permeability of porous rocks are advantageous over the previous approaches because these can express the stress dependency of both the porosity and the permeability of porous rocks by theoretically sound fully analytical equations. In contrast, the previous applications by Zhu et al. (2018) and Civan (2019a) only resulted in semi-analytical equations because the previous formulation employed a rather simple empirical equation for porosity variation by effective stress in their derivations of the stress-dependent permeability (see “Appendix”).
该文提出的孔隙率和渗透率机理模型及其导出的方程，相较于先前方法具有优势，因为这些方程能够通过理论严谨的完全解析方程表达孔隙率和渗透率的应力依赖性。相比之下，Zhu 等人（2018 年）和 Civan（2019a）的先前应用仅得到半解析方程，因为他们在推导应力相关渗透率时，使用了较为简单的经验方程来描述有效应力对孔隙率变化的影响（见“附录”）。

The classical bundle of tubes model applied in this paper yields very accurate correlations of the experimental data, as demonstrated by accurately analyzing and correlating the data of Jones et al. (2001) and Zhu et al. (2018). Nevertheless, some possible improvements on the classical Kozeny–Carman equation may be considered in future studies. In particular, investigation of some developments is recommended based on the bundle of leaky tubes interacting with cross-flow (Civan 2001, 2002, 2017) and the existence of micro-channels with different spatial orientations (Abdalrahman et al. 2015).
本文应用的经典管束模型在处理实验数据时，能够得到非常精确的相关性，这通过准确分析和关联 Jones 等人（2001 年）和 Zhu 等人（2018 年）的数据得到了证明。尽管如此，在未来的研究中，可以考虑对经典的 Kozeny-Carman 方程进行一些可能的改进。特别是，建议基于泄漏管束与交叉流相互作用（Civan 2001，2002，2017）以及存在不同空间取向的微通道（Abdalrahman 等人，2015 年）的发展进行调查。

Appendix: Semi-analytical Formulation of Stress-Dependent Porosity and Permeability of Porous Rocks
附录：应力依赖性多孔岩石孔隙率和渗透率的半解析公式

The stress dependence of porosity was approximated by the following empirical exponential decay equation by Zhu et al. (2018) and later by Civan (2019a). The linear dependence on the effective stress was expressed by a truncated Taylor series expansion and then using Eq. (10) as:
应力对孔隙率的影响通过以下经验指数衰减方程进行近似，由 Zhu 等人（2018 年）提出，后来由 Civan（2019a）进一步发展。有效应力对孔隙率的线性依赖性通过截断泰勒级数展开表示，然后使用公式（10）表示为：

$$\varphi ={\varphi }_{\text{o}}\exp \left[-c_{\text{p}}\left(p_{\text{o}}-p\right)\right]\cong {\varphi }_{\text{o}}\left[1-c_{\text{p}}\left(p_{\text{o}}-p\right)\right]={\varphi }_{\text{o}}\left[1+c_{\text{p}}\left(\frac{{\text{σ}}_{\text{o}}-\text{σ}}{\mathrm{X}}\right)\right]$$

(A-1)

Consequently, by applying Eq. (A-1), Civan (2019a) derived the following semi-analytic equation for stress-dependent permeability:
因此，通过应用公式（A-1），Civan（2019a）推导出了应力依赖性渗透率的以下半解析方程：

$$\frac{D^{\mathrm{\prime }}+\text{σ}}{K^{1/\phantom{14}4}}=a^{\mathrm{\prime }}{\text{σ}}^2+b^{\mathrm{\prime }}\text{σ}+c^{\mathrm{\prime }}$$

(A-2)

where a′, b′, c′, and D′ are some parameters.
其中 a′、b′、c′和 D′是一些参数。

Here, it is shown that Eq. (A-1) can be derived also by neglecting several terms in Eq. (14) and applying Eqs. (2) and (3) as the following.
这里，展示了可以通过忽略方程(14)中的几个项，并应用方程(2)和(3)来推导出方程(A-1)。

$$\begin{array}{rl}\text{σ}& =p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}-\frac{E\mathrm{X}}{1-\upsilon }\left[\frac{r_0{r}_2^2-r_0{r}_1^2-r_1{r}_2^2+r_1^3}{r_1^3+\left(\frac{1+\upsilon }{1-\upsilon }\right)r_2^2{r}_1}\right]\\ & \cong p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}-\frac{E\mathrm{X}}{1-\upsilon }\left[\frac{r_1^3}{\left(\frac{1+\upsilon }{1-\upsilon }\right)r_2^2{r}_1}\right]=p_{\text{o}}\mathrm{X}+{\text{σ}}_{\text{o}}-\frac{E\mathrm{X}{\alpha }^2}{\left(1+\upsilon \right)r_2^2}\varphi \end{array}$$

(A-3)

Solving Eq. (A-3) for porosity $\varphi$ yields the above given Eq. (A-1) as:

$$\begin{array}{rl}& \varphi =\frac{p_{\text{o}}\left(1+\upsilon \right)r_2^2}{E{\alpha }^2}\left[1+\frac{1}{p_{\text{o}}}\left(\frac{{\text{σ}}_o-\text{σ}}{\mathrm{X}}\right)\right]={\varphi }_{\text{o}}\left[1+c_{\text{p}}\left(\frac{{\text{σ}}_{\text{o}}-\text{σ}}{\mathrm{X}}\right)\right]\\ & \text{where }\\ & {\varphi }_{\text{o}}=\frac{p_{\text{o}}\left(1+\upsilon \right)r_2^2}{E{\alpha }^2},c_{\text{p}}=\frac{1}{p_{\text{o}}}\end{array}$$

(A-4)

This exercise reveals that Eq. (A-1) involves a significant simplification compared to the full mechanistic model developed in this paper.