This is a bilingual snapshot page saved by the user at 2024-12-23 18:05 for https://zhuanlan.zhihu.com/p/721097691, provided with bilingual support by Immersive Translate. Learn how to save?
  First published onLLM Reasonable
LLM Reasoning（十）：STaR的变种们

LLM Reasoning（十）：STaR的变种们

Jarlene
Jarlene
it
12 人赞同了该文章
​
  Directory
  Fold up
  Past Review
  Introduction
  Detailed introduction
STaR
Quiet-STaR
V-STaR
Kwai-STaR
Lean-STaR
RL-STaR

  Past Review


Jarlene: LLM Reasoning (Part 1): STaR


Jarlene: LLM Reasoning (Part 2): Quiet-STaR


Jarlene：LLM Reasoning (3): Q*


Jarlene: LLM Reasoning (Part 4): rStar


Jarlene：LLM Reasoning (5): TTC


Jarlene：LLM Reasoning (6): Let's Verify Step by Step

Jarlene：LLM Reasoning（七）：造数据（MiPS 、Math-Shepherd、OmegaPRM）

Jarlene：LLM Reasoning（八）： MCTS

Jarlene：LLM Reasoning（九）： MCTS+Self-Refine/DPO...

  Introduction


Originally planned to elaborate on llm agent for Reasoning techniques in the tenth issue, but recently while conducting various experiments, I found that there are many variants of the methods in STaR, so I want to discuss the variants of STaR separately, and then elaborate on the agent for Reasoning in the next issue.

  Detailed introduction

STaR


STaR aims to address how to improve the performance of language models in complex reasoning tasks, such as solving math problems or answering common sense questions. Its main feature is not relying on labeled data, but generating data through self-iterative models (CoT). The specific implementation steps are as follows:


  1. Initialization: Given a pre-trained large language model (LLM) M $$ M $$ and an initial set of questions D={(xi,yi)}i=1D $$ D = \{(x_i, y_i)\}_{i=1}^D $$, where xi $$ x_i$$ is the question, and yi $$y_i$$ is the answer. Additionally, there is a small example set P={(xpi,rpi,ypi)}i=1P P = \{(x_p^i, r_p^i, y_p^i)\}_{i=1}^P , where rpi $$ r_p^i $$ is the corresponding reasoning process.

  2. Rationale Generation: Using a small set of example prompts P $$ P $$ to guide the model M $$ M $$ to self-generate the rationale xi $$ x_i$$ for each question r^i $$\hat{r}_i $$ and the answer y^i $$ \hat{y}_i $$. This process can be represented as: (r^i,y^i)←Mn−1(xi) $$ (\hat{r}_i, \hat{y}_i) \leftarrow M_{n-1}(x_i)$$, where Mn−1 $$M_{n-1} $$ represents the model after the previous iteration.

  3. Correctness Check: For the generated inferences and answers, only retain those examples where the answers are correct, i.e.: Dn={(xi,r^i,yi)|i∈[1,D]∧y^i=yi} $$ D_n = \{(x_i, \hat{r}_i, y_i) | i \in [1, D] \land \hat{y}_i = y_i\}$$

  4. Fine-tuning: Perform fine-tuning on the retained correct example set Dn D_n for the model M $$M $$, obtaining the new model Mn $$M_{n} $$.

  5. Rationalization: For questions that the model failed to answer correctly, provide the correct answer as a hint to enable the model to generate corresponding reasoning. This process can be represented as: (r^rati,y^rati)←Mn−1(add_hint(xi,yi))for i∈[1,D]∧y^i≠yi $$ (\hat{r}_{\text{rat}}^i, \hat{y}_{\text{rat}}^i) \leftarrow M_{n-1}(\text{add_hint}(x_i, y_i)) \quad \text{for } i \in [1, D] \land \hat{y}_i \neq y_i$$. Here, the add_hint function is used to add the correct answer as a hint.

  6. Dataset Expansion: Add the generated rational inferences to the fine-tuning dataset Dn \(D_n\), that is: Dnrat={(xi,r^rati,yi)|i∈[1,D]∧y^i≠yi∧y^rati=yi} \(D^{rat}_n = \{(x_i, \hat{r}_{\text{rat}}^i, y_i) | i \in [1, D] \land \hat{y}_i \neq y_i \land \hat{y}_{\text{rat}}^i = y_i\}\). Then, merge Dn \(D_n\) and Dnrat \(D^{rat}_n\) to form the new fine-tuning dataset.
  7. 重复迭代：使用合并后的数据集对模型M 进行微调，然后重复步骤3到6，直到性能不再提升。

Quiet-STaR

Quiet-STaR旨在解决语言模型在处理文本时如何更有效地进行推理的问题。它试图解决计算成本、初始能力缺失、超越单个token的预测等问题。Quiet-STaR的原理是通过训练语言模型（LM）在生成每个token时都生成一个推理过程（rationale），从而提高模型对后续文本的预测能力。这种方法的核心思想是，通过在每个token后面插入一个推理步骤，可以帮助模型更好地理解和预测文本的深层含义。Quiet-STaR的工作原理可以概括为以下三个主要步骤：

  1. 并行推理生成（Parallel Rationale Generation）： 在输入序列的每个token后面，模型并行生成多个推理（rationales）。这些推理由特定的起始和结束标记（如<|startofthought|>和<|endofthought|>）标识。
  2. 混合推理和基础预测（Mixing Post-Rationale and Base Predictions）： 模型使用一个“混合头”（mixing head），这是一个浅层的多层感知机（MLP），它输出一个权重，决定在给定推理后生成的下一个token预测（logits）与基础语言模型预测之间的混合程度。
  3. 优化推理生成（Optimizing Rationale Generation）： 使用REINFORCE算法，根据推理对未来token预测的影响来优化推理生成参数。模型通过增加那些使未来文本预测更有可能的推理的可能性，同时减少那些使预测变得不太可能的推理的可能性，来提高推理的质量。

虽然Quiet-STaR通过一些技术手段解决这里面的问题，但是针对每个token都生成CoT的过程，成本也是异常大。最近笔者在使用结合token熵或者Routing的方式来动态选择token生成CoT的过程。这样可以有效的解决每个token都生成CoT的过程。

V-STaR

V-STaR数据构造流程图

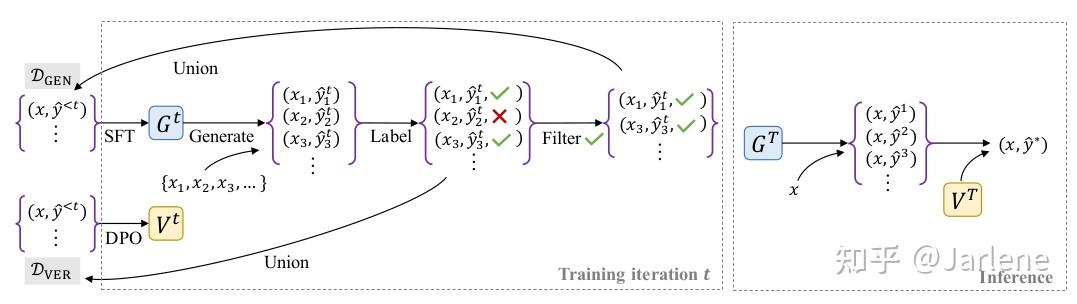
V-STaR尝试解决的问题是如何提高大型语言模型（LLMs）在复杂推理任务中的表现，特别是在代码生成和数学推理方面的能力。V-STaR核心思想是通过利用模型生成的正确和错误解决方案来训练一个验证器，并在推理时使用该验证器从多个候选解决方案中选择最佳的一个。具体步骤如下：

  1. 生成器训练：生成器 GG 是一个预训练的语言模型，通过监督微调（Supervised Fine-Tuning, SFT）在原始训练数据 DSFTD_{SFT} 上进行初始训练： LSFT(G)=−E(x,y)∼DSFT∑t=1Tlog⁡G(yt|y<t,x)\mathcal{L}_{\text{SFT}}(G) = -\mathbb{E}_{(x,y) \sim \mathcal{D}_{\text{SFT}}} \sum_{t=1}^{T} \log G(y_t | y_{<t}, x) ，其中 x\( x \) 是问题描述， y\( y \) 是解决方案，T是解决方案的长度。在每个迭代 t\( t \) 中，生成器 Gt\( G^t \) 从预训练模型 Gbase\( G_{\text{base}} \) 开始，使用增强的训练数据 DCEN\( \mathcal{D}_{\text{CEN}} \) 进行微调： Gt=SFT(Gbase,DCEN)G^t = \text{SFT}(G_{\text{base}}, \mathcal{D}_{\text{CEN}}) 。
  2. 验证器训练：验证器 V\( V \) 使用直接偏好优化（Direct Preference Optimization, DPO）方法进行训练。首先构建一个偏好数据集 Dpref\( \mathcal{D}_{\text{pref}} \) ，其中包含正确和错误解决方案的对： Dpref={(xi,yi,1+,yi,1−),⋯,(xi,yi,m+,yi,m−)}i=1N\mathcal{D}_{\text{pref}} = \{(x_i, y^{+}_{i,1}, y^{-}_{i,1}), \cdots, (x_i, y^{+}_{i,m}, y^{-}_{i,m})\}_{i=1}^{N} ，其中 y+\( y^{+} \) 是正确的解决方案， y−\( y^{-} \) 是错误的解决方案，m是每个问题的偏好对数量。使用DPO目标函数训练验证器 V\( V \) ： LDPO(V;GSFT)=−E(x,y+,y−)∼Dpref[log⁡σ(r^(x,y+)−r^(x,y−))]\mathcal{L}_{\text{DPO}}(V; G_{\text{SFT}}) = -\mathbb{E}_{(x, y^{+}, y^{-}) \sim \mathcal{D}_{\text{pref}}} \left[ \log \sigma \left( \hat{r}(x, y^{+}) - \hat{r}(x, y^{-}) \right) \right] ，其中 σ\( \sigma \) 是逻辑函数， r^(x,y)=βlog⁡V(y|x)GSFT(y|x)\( \hat{r}(x, y) = \beta \log \frac{V(y|x)}{G_{\text{SFT}}(y|x)} \) ， β\( \beta \) 是一个控制参考策略 GSFT\( G_{\text{SFT}} \) 接近程度的超参数。
  3. 迭代改进：在每个迭代中，生成器 Gt\( G^t \) 生成多个候选解决方案，并根据正确性标签进行标注。正确的解决方案被添加到生成器训练数据 DCEN\( \mathcal{D}_{\text{CEN}} \) 中，而所有解决方案（正确和错误）被添加到验证器训练数据 DVER\( \mathcal{D}_{\text{VER}} \) 中。通过多次迭代，生成器和验证器逐步改进，最终生成器 GT\( G^T \) 和验证器 VT\( V^T \) 在推理时用于生成和评估候选解决方案。

在推理时，生成器GT\( G^T \)生成多个候选解决方案，验证器VT\( V^T \)对这些解决方案进行评分，并选择评分最高的解决方案作为最终答案。最佳解决方案的准确率可以通过以下公式计算： Best-of-k:=1(Nk)∑l=0N−k(N−i−1k−1)ai\text{Best-of-}k := \frac{1}{\binom{N}{k}} \sum_{l=0}^{N-k} \binom{N-i-1}{k-1} a_i ，其中 [a0,…,aN−1]\( [a_0, \ldots, a_{N-1}] \) 是按验证器评分排序的候选解决方案的正确性标签，N是候选解决方案的总数，k是选择的解决方案数量。

V-STaR可以简单认为是SPIN+GAN+STaR的思想。这里的STaR可能是只是利用到它造数据的部分功能，当然也可以是我们之前讲述过得LLM Reasoning（七）：造数据（MiPS 、Math-Shepherd、OmegaPRM）

Kwai-STaR

文章认为现有的方法已经取得了显著进展，但大多数方法并未充分利用状态转移（state transition）在LLM推理中的价值。Kwai-STaR通过将LLMs转化为状态转移推理器（State-Transition Reasoners），来提高其直观的推理能力。Kwai-STaR首先针对状态空间进行了定义，主要分成三部分：

  • 状态（State）：问题解决过程中的特定点，从初始状态（原始问题）到最终状态（正确答案）。
  • 状态转移推理器（State-Transition Reasoner）：通过执行动作集中的操作，从初始状态转移到最终状态的LLM。
  • 动作（Action）：推理器执行的操作，包括形式化（Formalize）、分解（Decompose）、解决子问题（Solve Subques）、解决父问题（Solve Parent）、验证（Verify）、回溯（Backtrack）和总结（Summarize）。

状态空间的设计遵循分治原则，推理器首先将原始问题形式化为数学表达式，然后分解为多个子问题并分别解决，最后结合子问题的答案解决原始问题。如果生成错误的中间结果，推理器会执行验证动作并回溯到上一个正确状态。这部分实现过程全靠Prompt。

同时Kwai-STaR提出状态转移数据构建的方法，其主要通过两阶段来构建：

  • 阶段I：生成器在没有验证和回溯动作的情况下解决问题，生成正确案例。这个过程是生成器根据预定义的动作集（如形式化、分解、解决子问题等）逐步解决问题，生成正确的状态转移路径。
  • 阶段II：对于生成器和微调模型在训练集上的错误案例，提供参考答案并指导生成器使用完整的动作集进行修正，生成错误-验证对。生成器首先生成错误的状态转移路径 yry_r ，然后根据参考答案 yrefy_{ref} 进行修正，生成正确的状态转移路径 yay_a 。错误状态转移路径yry_r和修正后的状态转移路径yay_a自然形成接受-拒绝对 <ya,yr><y_a,y_r> ，这些对用于后续的高级精炼阶段（Advanced Refinement）中的直接偏好优化（DPO）训练。

模型训练部分也采用两阶段训练方法：

  • 基础训练阶段（Fundamental Training）：使用阶段I的正确案例进行监督微调（SFT），帮助模型掌握状态转移方式。采用常见的下一个token预测损失函数： LNTP=−∑t=1Tlog⁡P(yt∣y<t;θ)\mathcal{L}_{\text{NTP}} = -\sum_{t=1}^{T} \log P(y_{t} \mid y_{<t}; \theta) ，其中 yt\( y_{t} \) 是第 t个token， y<t\( y_{<t} \) 是前t-1个token， θ\( \theta \) 是模型参数。

Kwai-STaR和V-STaR处理思路类似，但是V-STaR采用SPIN这种迭代的思路，而在Kwai-STaR中却没有这种情况。

Lean-STaR

Lean-STaR流程图

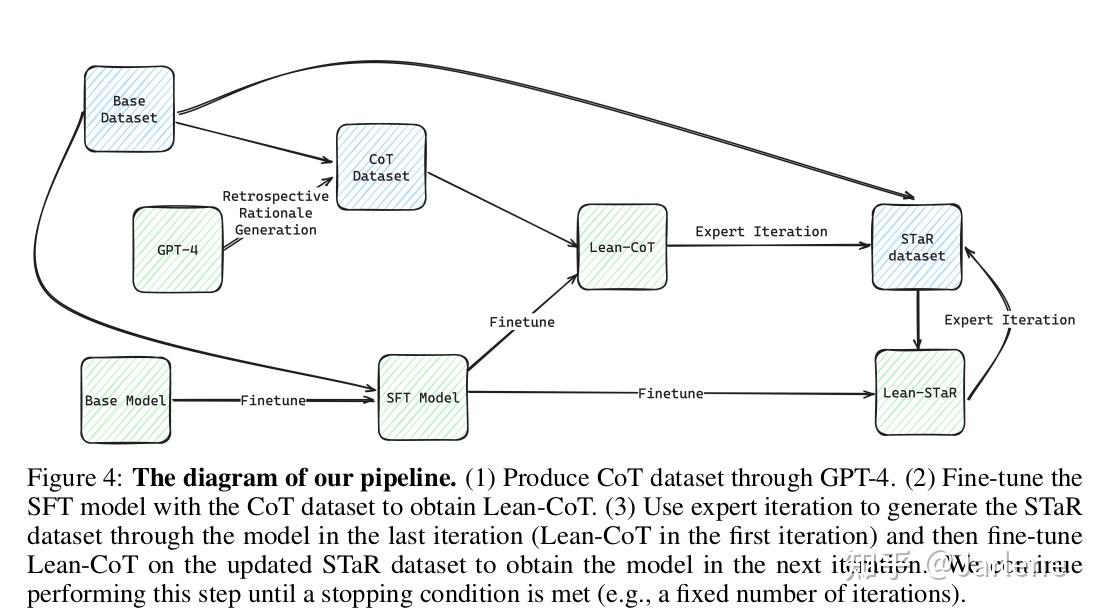
这篇文章尝试解决的问题是如何通过结合非正式的思考过程来增强语言模型在形式化定理证明中的能力。传统的基于语言模型的定理证明方法通常只依赖于形式化证明数据进行训练，而忽略了大量有用的非正式信息。Lean-STaR主要包括三步：

1. 生成合成思维（Retrospective Rationale Generation）：Lean-STaR首先通过回顾性的真实策略生成合成思维。具体步骤如下：

  • 定义问题：将定理证明问题定义为一个马尔可夫决策过程（Markov Decision Process, MDP），其中证明状态（state）和策略（action）分别对应于MDP中的状态和动作。

2. 推理增强的策略预测（Thought-augmented Tactic Prediction）:在推理时，训练好的模型在预测每个证明步骤的策略之前直接生成思维。具体步骤如下：

  • 训练模型：使用生成的(状态, 思维, 策略)对进行训练，得到推理增强的策略预测模型。


  • 采样和验证：使用当前模型 M对每个问题进行 K次采样，生成证明轨迹，并过滤出成功的证明轨迹。
  • 迭代：重复上述步骤，直到满足停止条件。

数学上，可以表示为： J(M,D)=∑iE(s0,t0,a0),⋯,(sn,tn,an)∼πM(|si)R((s0,t0,a0),⋯,(sn,tn,an))\[ J(M, D) = \sum_i \mathbb{E}_{(s_0, t_0, a_0), \cdots, (s_n, t_n, a_n) \sim \pi_M(|s^i)} R\left((s_0, t_0, a_0), \cdots, (s_n, t_n, a_n)\right) \] ，其中 J(M,D)\( J(M, D) \) 是总期望奖励， R\( R \) 是奖励函数， πM\( \pi_M \) 是模型的策略。

RL-STaR

RL-STaR的核心原理是将链式思维（Chain-of-Thought, CoT）推理过程建模为一个强化学习问题。推理过程被视为一个状态转移过程，模型在每个步骤中根据当前状态选择一个动作（即生成一个推理步骤），并根据最终的推理结果获得奖励。通过不断迭代训练，模型逐步改进其推理策略，使其能够生成更准确的推理步骤。

定义强化学习的状态、动作和奖励：

  • 状态： SnS_n 表示第n步的状态， S0S_0 ​是初始状态， SnS_n 是最终状态。
  • 动作：A表示模型在每个步骤中生成的推理步骤。
  • 策略： π(A|S)\(\pi(A|S)\) 表示模型在给定状态S下选择动作A的概率。
  • 转移函数： P(Sn+1|A,Sn)\(P(S_{n+1}|A, S_n)\) 表示在状态SnS_n下采取动作A后转移到状态Sn+1S_{n+1}的概率。
  • 奖励：在最终状态SnS_n时，如果生成的推理结果与正确答案匹配，则奖励为1，否则为0。

RL-STaR的实现主要包括以下几个步骤：

  1. RL-CoT生成推理步骤和轨迹：
    1. 初始化轨迹 τ=(s0)\(\tau = (s_0)\) 。
    2. 对于每个步骤 n\(n\) 从1到N：（1）根据策略 π(A|Sn−1=sn−1)\(\pi(A|S_{n-1} = s_{n-1})\) 输出动作 A=sn\(A = s_n\) 。（2）确定下一个状态 sn\(s_n\) ，因为转移函数是确定性的，满足 P(Sn=sn|A=sn,Sn−1=sn−1)=1\(P(S_n = s_n|A = s_n, S_{n-1} = s_{n-1}) = 1\) 。（3）将 sn\(s_n\) 添加到轨迹 τ\(\tau\) 中。
    3. 返回最终状态 sN\(s_N\) 和轨迹τ\(\tau\)。
  2. 训练迭代模型：
    1. 初始化训练数据集 Dtrain\(\mathcal{D}_{\text{train}}\) 和预训练的LLM策略 π0\(\pi_0\) 。
    2. 对于每个训练迭代 t\(t\) 从1到T：（1）运行RL-CoT算法生成最终状态 sN\(s_N\) 和轨迹 τ\(\tau\) 。（2）收集那些最终状态与正确答案匹配的轨迹。（3）使用这些轨迹训练LLM策略，得到新的策略 πt\(\pi_t\) 。

RL-STaR在文章中提供了比较完整的理论分析，但是这篇文章没有提供完整实验情况。所有我个人对这篇文章实用性大打折扣。

发布于 2024-12-23 12:07・IP 属地北京

内容所属专栏

「真诚赞赏，手留余香」
还没有人赞赏，快来当第一个赞赏的人吧！
LLM
reasoning
STAR
理性发言，友善互动

还没有评论，发表第一个评论吧
想来知乎工作？请发送邮件到 jobs@zhihu.com