AI technology, represented by large models, has been unprecedentedly prosperous in the past two years. We believe that in such a context, it is necessary to start learning from the most basic concepts, and gradually establish a relatively complete knowledge system in order to understand the subsequent new concepts, new technologies, and new products. Therefore, this article is written to discuss the most basic concepts in the knowledge system of large models, and to pave the way for the subsequent articles in this series.
For the construction of a large model knowledge system, I think we need to understand the following issues first:
(1) Regardless of whether it is a large model or a small model, can you first explain what a model is?
(2) How exactly is the model trained with data, so that the trained model can be used to solve practical problems?
I will use a practical problem of predicting milk tea sales as a starting point, design and manually train a simplest model, and discuss the above two core questions step by step along the way.
A model is essentially a mathematical formula, or more precisely, a function. Training a model is the process of using data to continuously update model parameters through a backpropagation algorithm to fit existing data. And because the trained model fits the existing data, we believe that it has mastered the statistical rules of the existing data, and then we can use this model (this law) to predict unknown situations.
"Dating an AI is like going on a 100-date date: it writes down everything you say as a cheat sheet and ends up with a love brain that understands you"
Let's say you work in a bubble tea shop, and the selling prices and sales of the 6 types of milk teas that have been on sale recently are as follows
One day, the boss asked you, if a new milk tea is launched at this time, if it is priced at 35 without considering other factors, how much should it sell? In other words, if the selling price is set at 35, how much do you predict to sell?
Damn, the price of 35 is not within the scope of the existing data at all, how can this be done?
Of course, we don't want to make predictions out of thin air, but to make predictions that are most in line with the current data laws based on the existing data, otherwise the boss will be dumb if we ask one more why. Let's take a look at the data first, and it is not difficult to find that the higher the selling price, the lower the sales volume.
900
850
800
Xinjiang residence
750
700
650
009
20
5
15
selling price
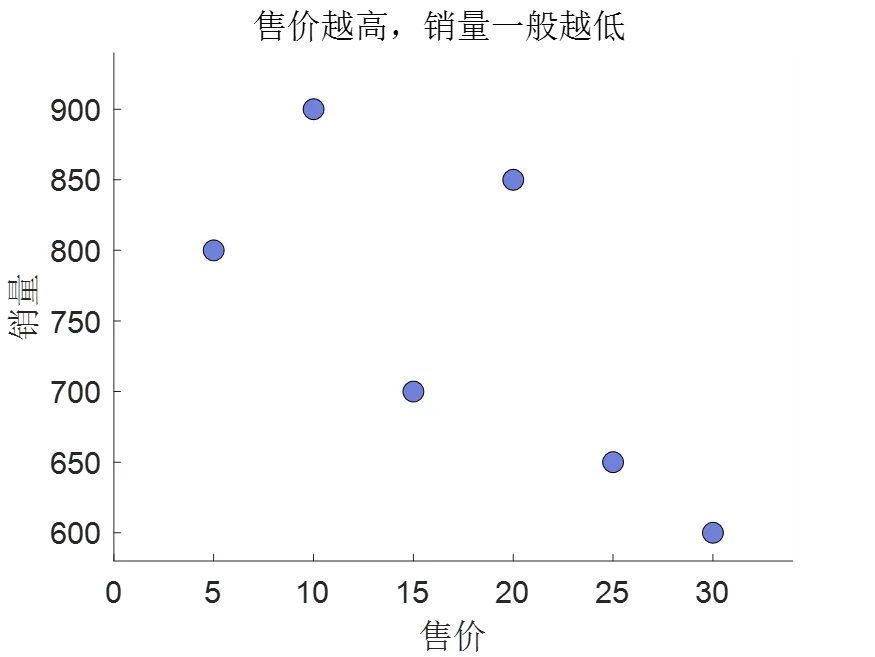
Imagine, if there is a mathematical formula that can directly tell us how much the specific sales volume corresponding to different selling prices are, then the sales volume when the predicted selling price is 35 is not a bag to pick up things, hand to catch, hand to pinch?
But how do you find this mathematical formula? If we look closely at the graph above, we can see the selling price as the independent variable and the sales volume as the dependent variable, and the dependent variable decreases with the increase of the independent variable, which can be completely used as a function that we learned in the second grade of junior high school
are the two parameters in this formula for which specific values have not yet been determined. Once we can be sure
In other words, we build a mathematical model for predicting the sales of milk tea:
Wait...... Model? Parameter? Forecast? Could it be that what kind of large model do you usually hear, and hundreds of millions of parameters refer to this?
That's right! A large model is essentially a mathematical formula with an extremely complex form and an extremely large number of parameters. And the so-called forecast, just like the sales volume after we give the selling price, is just given a specific input and then calculated according to the formula.
3 人点赞
3




