梯度下降用于不可微问题：分布采样随机数、argmax、Clip函数、强化学习

心火试新茶

天天向上，天天快乐

18 人赞同了该文章

发布于 2024-07-20 10:06・IP 属地四川，编辑于 2024-08-04 13:52・IP 属地四川

收起

引言

重参数化技巧-分布采样随机数的梯度优化

独立正态分布

协方差正态分布

均匀分布

Argmax取最大值的梯度优化

硬（Hard Gumbel-Softmax）

软（Soft Gumbel-Softmax）

整合代码实现:

Clip截断函数(min、max)的梯度优化

代理损失函数（Surrogate Loss Function）

强化学习 (目标函数零梯度)

策略梯度法

从策略梯度算法到Actor - Critic算法的动机

PPO算法

引言

许多实际问题中涉及到的操作并非梯度可传递，例如分布采样随机数、argmax操作、Clip函数(如min和max等)。

为了能在这种问题中应用梯度下降优化，研究者提出了多种创新性的方法来克服这些问题，例如重新参数化技巧（reparameterization trick）、梯度估计方法、以及平滑近似技术等。

本文将探讨在梯度不可传递问题的梯度优化解决方案，具体分析：

分布采样随机数
argmax操作
Clip截断函数(如min和max等)
强化学习 (目标函数零梯度)

这些问题在梯度优化中的处理方法。

重参数化技巧-分布采样随机数的梯度优化

在深度学习中的变分编码器、PPO-连续动作算法中，都涉及到了分布采样随机数生成机制。

随机数的生成过程，其实也可以是一个梯度可传递的过程。

尽管在生成随机数的过程中，标准的随机数生成函数并不是可微的（即没有梯度）。

但是，可以通过重新参数化技巧（reparameterization trick）来实现随机数生成过程的可微性，从而使梯度能够传播。

重新参数化技巧的核心思想是将随机变量的生成过程表示为一个确定性的函数加上一个随机噪声，这样就可以通过对确定性函数求导来获得梯度。

独立正态分布

假设我们有一个正态分布 $N (μ, σ^{2})$ N(\mu, \sigma^2) ，我们希望从中采样。通过重新参数化技巧，可以将采样过程表示为：

$z = μ + σ \cdot ϵ$ \[ z = \mu + \sigma \cdot \epsilon \]

其中 $ϵ \sim N (0, 1)$ \epsilon \sim N(0, 1) \ 是从标准正态分布中采样的随机变量。由于 mu和 sigma 是确定性的，所以这个表达式是可微的。

在 PyTorch 中，可以这样实现：

```python
import torch

# 参数
mu = torch.tensor(0.0, requires_grad=True)
sigma = torch.tensor(1.0, requires_grad=True)

# 从标准正态分布中采样
epsilon = torch.randn(1)

# 重新参数化
z = mu + sigma * epsilon

# 打印生成的随机数
print(z)

# 假设我们有一个损失函数，例如 z 的平方
loss = z ** 2

# 反向传播
loss.backward()

# 打印梯度
print(mu.grad)
print(sigma.grad)
```

协方差正态分布

注记：对于任何高维高斯 $x \sim N (x | μ, Σ)$ \mathbf{x} \sim \mathcal{N}(\mathbf{x}|\boldsymbol{\mu},\boldsymbol{\Sigma}) ， $Σ$ {\Sigma} 是多元变量分布的协方差矩阵，采样过程可以直接对白噪声进行变换：

$x = μ + Σ^{\frac{1}{2}} w$ \mathbf{x} = \boldsymbol{\mu} + \boldsymbol{\Sigma}^{\frac{1}{2}}\mathbf{w}\\其中 $w \sim N (0, I)$ \mathbf{w} \sim \mathcal{N}(0,\mathbf{I}) ，协方差矩阵矩阵的平方根 $Σ^{\frac{1}{2}}$ \boldsymbol{\Sigma}^{\frac{1}{2}} 可以通过协方差矩阵特征分解或 Cholesky 分解得到。

在很多情况下，简化为样本彼此独立分布的情况，此时协方差矩阵的非对角元素都是0，也就是对角矩阵 $Σ = σ^{2} I$ \boldsymbol{\Sigma} = \sigma^2\mathbf{I} ， $σ$ \sigma 同样为对角矩阵。

对于对角矩阵 $Σ = σ^{2} I$ \boldsymbol{\Sigma} = \sigma^2\mathbf{I} ，上述公式可简化为

$x = μ + σ w$ \mathbf{x} = \boldsymbol{\mu} + \sigma\mathbf{w} \qquad \\

均匀分布

对于均匀分布 U(a, b)，可以类似地进行重新参数化。假设我们有一个均匀分布 $ U(a, b) $，可以将采样过程表示为：

$z = a + (b - a) \cdot ϵ$ z = a + (b - a) \cdot \epsilon

其中 $ϵ \sim U (0, 1)$ \epsilon \sim U(0, 1) \ 是从标准均匀分布中采样的随机变量。

在 PyTorch 中，可以这样实现：

```python
import torch

# 参数
a = torch.tensor(0.0, requires_grad=True)
b = torch.tensor(1.0, requires_grad=True)

# 从标准均匀分布中采样
epsilon = torch.rand(1)

# 重新参数化
z = a + (b - a) * epsilon

# 打印生成的随机数
print(z)

# 假设我们有一个损失函数，例如 z 的平方
loss = z ** 2

# 反向传播
loss.backward()

# 打印梯度
print(a.grad)
print(b.grad)
```

通过重新参数化技巧，我们可以使从分布中生成随机数的过程变得可微，从而能够在深度学习模型中传播梯度。这种方法在变分自编码器、PPO-连续动作算法等中非常常见。

Argmax取最大值的梯度优化

Gumbel-Softmax是一种在深度学习中用于离散分布采样的技巧，它允许梯度通过采样操作传播，从而能够在训练过程中优化离散变量。这种方法有两个主要版本：软版本（Soft Gumbel-Softmax）和硬版本（Hard Gumbel-Softmax）。以下是对这两个版本的介绍。

硬（Hard Gumbel-Softmax）

硬版本的Gumbel-Softmax进一步将软版本的输出离散化，通过使用argmax操作来选择概率最大的类别，并生成一个one-hot向量。然而，argmax操作本身不可微，因此硬版本采用了一种取巧的方式，即在前向传播中使用argmax，但在反向传播中依然使用软版本的连续输出。

采样one-hot向量：在前向传播中，使用argmax操作从softmax软版本的输出中选择最大概率的索引。
梯度传播：在反向传播中，梯度依然通过软版本的输出传播，从而保持整个过程的可微性。

这种方法被称为“硬Gumbel-Softmax”（Hard Gumbel-Softmax），它结合了离散样本的优点，同时保持了训练过程中的可微性。

具体代码实现：

_, max_idx = y_softmax.max(dim=-1, keepdim=True)

y_hard = torch.zeros_like(y_softmax).scatter_(-1, max_idx, 1.0)

y = y_hard - y_softmax.detach() + y_softmax

其中，y_hard表示的是通过argmax操作得到的one-hot向量。y_softmax表示原始的Softmax向量。

最核心的：y = y_hard - y_softmax.detach() + y_softmax

这行代码的作用是：

y_softmax.detach() 返回一个从计算图中分离的y_softmax，即不进行梯度传播。
y_hard - y_softmax.detach() + y_softmax的目的是在前向传播中使用离散的y_hard，但在反向传播中使用连续的y_softmax，从而保持梯度的可传播性。

软（Soft Gumbel-Softmax）

软版本的Gumbel-Softmax是通过引入Gumbel噪声来实现对离散变量的连续近似。其主要目的是生成一组概率分布，这些概率分布可以用来近似离散样本。具体来说：

1. Gumbel噪声的引入：给定一个概率分布 $π$ $\pi$ ，首先对每个类别 i 添加一个Gumbel噪声 $g_{i}$ $g_i$ ，使得：

$g_{i} = - \log (- \log (U_{i}))$ g_i = -\log(-\log(U_i))

其中 U_i 是从均匀分布 U(0, 1)中采样的随机变量。

2. Gumbel-Softmax采样：然后通过Softmax函数进行处理，得到新的概率分布：

$y_{i} = \frac{\exp ((\log (π_{i}) + g_{i}) / τ)}{\sum_{j = 1}^{k} \exp ((\log (π_{j}) + g_{j}) / τ)}$ y_i = \frac{\exp((\log(\pi_i) + g_i) / \tau)}{\sum_{j=1}^k \exp((\log(\pi_j) + g_j) / \tau)}

其中 $τ$ \tau\ 是一个温度参数，控制输出分布的平滑程度。较低的 $τ$ \tau 值会使输出更接近于一个one-hot向量。

软版本的Gumbel-Softmax的输出是一个连续的概率分布，可以直接用于反向传播，因此在训练过程中是可微的。

整合代码实现:

import torch
import torch.nn.functional as F

def sample_gumbel(shape, eps=1e-20):
    U = torch.rand(shape)
    return -torch.log(-torch.log(U + eps) + eps)

def gumbel_softmax_sample(logits, temperature):
    gumbel_noise = sample_gumbel(logits.size())
    y = logits + gumbel_noise
    return F.softmax(y / temperature, dim=-1)

def gumbel_softmax(logits, temperature, hard=False):
    y_soft = gumbel_softmax_sample(logits, temperature)
    
    if hard:
        # 通过one-hot编码进行离散化
        shape = y_soft.size()
        _, max_idx = y_soft.max(dim=-1, keepdim=True)
        y_hard = torch.zeros_like(y_soft).scatter_(-1, max_idx, 1.0)
        
        # 在反向传播中通过y_soft传播梯度
        y = y_hard - y_soft.detach() + y_soft
    else:
        y = y_soft
    
    return y

# 示例用法
logits = torch.randn(3, 5)  # 3个样本，每个样本有5个类别的logits
temperature = 0.5

# 软版本Gumbel-Softmax
y_soft = gumbel_softmax(logits, temperature, hard=False)
print("Soft Gumbel-Softmax:\n", y_soft)

# 硬版本Gumbel-Softmax
y_hard = gumbel_softmax(logits, temperature, hard=True)
print("Hard Gumbel-Softmax:\n", y_hard)

Clip截断函数(min、max)的梯度优化

代理损失函数（Surrogate Loss Function）

clip函数常见的是取最小和最大值的min和max函数

如果边界是常数，而非有梯度的函数的话(比如PPO算法中的的clip是函数) ，clip函数的边界是梯度不可传递的。

可以采用平滑逼近的方法来使其可以传递梯度。

这种方法被叫做代理损失函数法（Surrogate Loss Function）

比如Sigmoid函数，输出范围是[0, 1]；Tanh函数的输出范围是[-1, 1]；

可以对Sigmoid函数、Tanh函数的输出进行缩放和平移，以实现最终所需要的最大、最小限制的目的。

或者使用

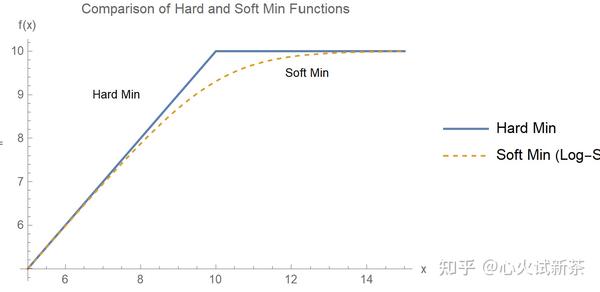
$m a x - l o g [1 + E x p [m a x - f (x)]]$ max - log[ 1+ Exp[max - f(x) ] ]

来限制输出范围是从 -∞ 到 max 的区间。（对于最小值的情况同理）

如图所示，这里的soft min是 10 - Log[1 + Exp[10 - x]]

强化学习 (目标函数零梯度)

策略梯度法

策略梯度方法是一类直接优化策略参数以最大化预期回报的算法。其核心思想是通过计算策略梯度来更新策略参数，使得策略的表现逐渐优化。常见的策略梯度方法包括REINFORCE算法、Actor-Critic算法以及TRPO（Trust Region Policy Optimization）等。

REINFORCE算法：一种策略梯度方法，通过蒙特卡洛方法估计梯度，直接优化策略参数以最大化累计奖励。

REINFORCE算法是策略梯度方法中的一种，用于解决强化学习中的策略优化问题。它通过直接优化策略参数来最大化累计奖励。REINFORCE的核心思想是利用蒙特卡洛方法估计梯度，从而更新策略参数。

1. 策略（Policy）：定义智能体在给定状态下选择动作的概率分布。通常表示为 $π_{θ} (a | s)$ $\pi_\theta(a|s)$ ，其中 $θ$ $\theta$ 是策略的参数。

这里详细讲一下 $π_{θ} (a_{t} | s_{t})$ $\pi_\theta(a_t | s_t)$ 。

离散动作：在动作空间离散的情况下，在给定的状态st ，Actor网络对于不同的动作类型，输出该动作类型中n个可能的动作空间softmax矩阵。为了能够让模型进行探索，一般并不对该softmax矩阵选取最大概率的直接输出。而是使用torch.distributions 的 Categorical 也就是“分类分布”来生成随机数，并用log_prob函数来反向获取这个action在分布中所对应的log概率，也就是 $\log π_{θ} (a_{t}^{i} | s_{t}^{i})$ \log \pi_\theta(a_t^i | s_t^i) 。

代码如下。dist.log_prob函数是可微的。策略梯度算法最后计算梯度用到的是log_prob。

from torch.distributions import Categorical
    action_probs = policy(state)
        # 采样策略：根据概率分布进行采样
        dist = Categorical(action_probs)
        action = dist.sample().item()
        log_prob = dist.log_prob(torch.tensor(action))

连续动作：在动作空间连续的情况下，在给定的状态st ，Actor网络对于不同的动作类型，通过上文中提到的重参数法，根据有梯度mu和sigma，来生成可微的正态分布采样下的随机数。同上，log_prob函数来反向获取这个action在分布中所对应的log概率，也就是 $\log π_{θ} (a_{t}^{i} | s_{t}^{i})$ \log \pi_\theta(a_t^i | s_t^i) 。dist.log_prob函数是可微的。策略梯度算法最后计算梯度用到的是log_prob。

from torch.distributions import Normal
   mu, sigma = policy(state)
    dist = Normal(mu, sigma)
    action = dist.sample()
    log_prob = dist.log_prob(action)

2. 回报（Return）：从当前时间步开始到最终结束所获得的累计奖励，记为 $R_{t}$ $R_t$ 。

这里的Return是由环境所提供的反馈，对于模型来说是零梯度的。

3. 优势函数（Advantage Function）：评估一个动作相对于策略中的平均动作好多少。

算法步骤

1. 采样轨迹：从当前策略 $π_{θ}$ $\pi_\theta$ 中采样多个轨迹 $(s_{0}, a_{0}, r_{0}, s_{1}, a_{1}, r_{1}, \dots, s_{T}, a_{T}, r_{T})$ $(s_0, a_0, r_0, s_1, a_1, r_1, \ldots, s_T, a_T, r_T)$ 。

2. 计算回报：对于每个时间步 $t$ $t$ ，计算从时间步 $t$ $t$ 开始的累计回报 $R_{t} = \sum_{k = t}^{T} γ^{k - t} r_{k}$ R_t = \sum_{k=t}^T \gamma^{k-t} r_k ，其中 $γ$ $\gamma$ 是折扣因子。

3. 计算梯度：利用蒙特卡洛方法估计梯度。梯度估计公式为：

$\nabla_{θ} J (θ) \approx \frac{1}{N} \sum_{i = 1}^{N} \sum_{t = 0}^{T} \nabla_{θ} \log π_{θ} (a_{t}^{i} | s_{t}^{i}) R_{t}^{i}$ \nabla_\theta J(\theta) \approx \frac{1}{N} \sum_{i=1}^N \sum_{t=0}^T \nabla_\theta \log \pi_\theta(a_t^i | s_t^i) R_t^i

其中， $N$ $N$ 是采样轨迹的数量。

4. **更新策略参数**：使用梯度下降法更新策略参数：

$θ \leftarrow θ - α \nabla_{θ} J (θ)$ \theta \leftarrow \theta - \alpha \nabla_\theta J(\theta)

其中， $α$ $\alpha$ 是学习率。

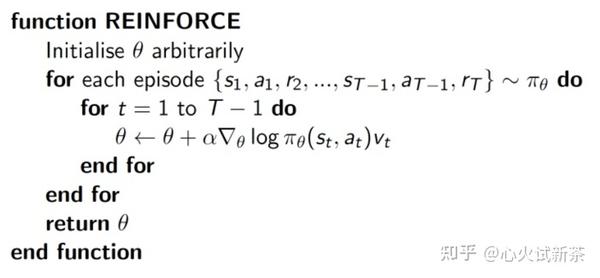
代码示例（ChatGPT 4o生成）

以下是使用PyTorch实现离散空间REINFORCE算法的示例代码：

```python
import torch
import torch.nn as nn
import torch.optim as optim
from torch.distributions import Categorical

class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim):
        super(PolicyNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, 128)
        self.fc2 = nn.Linear(128, action_dim)
    
    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.softmax(self.fc2(x), dim=-1)
        return x

def select_action(policy, state):
    state = torch.from_numpy(state).float()
    probs = policy(state)
    m = Categorical(probs)
    action = m.sample()
    return action.item(), m.log_prob(action)

def train(policy, optimizer, trajectories, gamma=0.99):
    policy_losses = []
    returns = []

    for trajectory in trajectories:
        rewards = trajectory['rewards']
        log_probs = trajectory['log_probs']
        R = 0
        returns = []
        
        for r in rewards[::-1]:
            R = r + gamma * R
            returns.insert(0, R)
        
        returns = torch.tensor(returns)
        returns = (returns - returns.mean()) / (returns.std() + 1e-5)

        for log_prob, R in zip(log_probs, returns):
            policy_losses.append(-log_prob * R)

    optimizer.zero_grad()
    policy_loss = torch.cat(policy_losses).sum()
    policy_loss.backward()
    optimizer.step()

# 示例用法
state_dim = 4  # 示例状态维度
action_dim = 2  # 示例动作维度
policy = PolicyNetwork(state_dim, action_dim)
optimizer = optim.Adam(policy.parameters(), lr=0.01)

# 采样轨迹并训练策略网络
# trajectories = [{'states': [...], 'actions': [...], 'rewards': [...], 'log_probs': [...]}]
# 在实际应用中，应该从环境中采样轨迹
# train(policy, optimizer, trajectories)
```

从策略梯度算法到Actor - Critic算法的动机

PPO算法

PPO算法介绍

Proximal Policy Optimization (PPO) 算法是当前强化学习问题广泛使用的方法，属于策略梯度方法中Actor - Critic的一种。PPO通过引入策略更新的限制来提高策略优化过程的稳定性和效率，被认为是简单但有效的策略优化算法。

PPO算法是对TRPO算法的一种改进，旨在解决TRPO实现复杂、计算开销大的问题。PPO通过引入目标函数的裁剪机制，在保证策略稳定性的同时，简化了优化过程。

PPO算法有两种常见的目标函数形式：PPO-Clip和PPO-Penalty。我们主要介绍PPO-Clip的目标函数。

PPO-Clip的目标函数定义为：

$L^{C L I P} (θ) = E_{t} [min (r_{t} (θ) {\hat{A}}_{t}, clip (r_{t} (θ), 1 - ϵ, 1 + ϵ) {\hat{A}}_{t})]$ \[ L^{CLIP}(\theta) = \mathbb{E}_t \left[ \min \left( r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t \right) \right] \]

其中：

- $r_{t} (θ) = \frac{π_{θ} (a_{t} | s_{t})}{π_{θ_{old}} (a_{t} | s_{t})}$ $ r_t(\theta) = \frac{\pi_\theta(a_t | s_t)}{\pi_{\theta_{\text{old}}}(a_t | s_t)} $ 是当前策略与旧策略的概率比。

- ${\hat{A}}_{t}$ \hat{A}_t\ 是优势函数。

- $ϵ$ \epsilon\ 是一个小的超参数，通常在0.1到0.2之间。

算法步骤：

1. **初始化**：初始化策略参数 $θ$ $\theta$ 和价值函数参数。

2. **采集数据**：使用当前策略与环境进行交互，收集状态、动作、奖励、以及状态值等数据。

3. **计算优势函数**：使用价值函数估计每个时间步的优势函数 ${\hat{A}}_{t}$ $\hat{A}_t$ 。

4. **优化策略**：通过梯度下降优化PPO目标函数，更新策略参数 $θ$ $\theta$ 。

5. **更新价值函数**：通过最小化均方误差（MSE）来更新价值函数参数。

6. **重复步骤2-5**：直至收敛。

发布于 2024-07-20 10:06・IP 属地四川，编辑于 2024-08-04 13:52・IP 属地四川

深度学习（Deep Learning）

变分自编码器

PPO算法

梯度下降用于不可微问题：分布采样随机数、argmax、Clip函数、强化学习

引言

重参数化技巧-分布采样随机数的梯度优化

独立正态分布

协方差正态分布

均匀分布

Argmax取最大值的梯度优化

硬（Hard Gumbel-Softmax）

软（Soft Gumbel-Softmax）

整合代码实现:

Clip截断函数(min、max)的梯度优化

代理损失函数（Surrogate Loss Function）

强化学习 (目标函数零梯度)

策略梯度法

从策略梯度算法到Actor - Critic算法的动机

PPO算法

文章被以下专栏收录

机器学习：分析实际，拒绝眼高手低无脑背书

推荐阅读

线性回归求解中梯度下降法与最小二乘法的比较

从为什么梯度方向是函数变化率最快方向详谈梯度下降算法

用人话讲明白梯度下降Gradient Descent（以求解多元线性回归参数为例）

线性回归之梯度下降与最小二乘法比较