解 説
マグネトグラフィ Retry Reason
(1997.4.1 受理)
Magnetography Retry Reason
Norio KOKAJI* Retry Reason
1.はじめに Retry Reason
マグネトグラフィは磁気の持つ安定性や記憶機能を利用するものであって,いったん潜像を記録すると,繰り返し現像•転写することができ,いわゆるマルチコピー が大量かつ高速に得られるという特徴を有するプリント方式である。
Retry
Reason
トナーを使い,潜像記録,現像,転写,定着というプ ロセスを経てハードコピーを得るという点で,電子写真 と似ているが,静電気と磁気の本質的な違いが,画像形成プロセスを異なるものにしている。最も大きな違い は,静電気が( + )または( - )の単極で存在するのに対し て,磁気は常に N,S 両極が一体になって存在するこ とである。本稿では主に筆者らの開発したシステムに基 づいてマグネトグラフィの画像形成プロセスを論ずる。始めに記録媒体からトナーにどのような力が働くかを論 じ,次いで記録媒体上の磁気潜像がトナーによって可視像化されるプロセスを説明し,次いでトナーについて述 べる。最後に今後の課題と展望に触れる。なお,磁気学 の慣例として,図中 N 極を+で, S 極を—で表示して あるので,電気の,
2.記録媒体から磁性トナーに働く磁気力 Retry Reason
2.1 原理
Fig. 1 に示すように磁化の向きを反転させて記録する と記録媒体上の転移領域に体積磁荷密度
れ,磁性トナー内部に磁荷が誘導される。その結果,磁性トナーは記録媒体に近い側で異極同士の吸引力を受け るとともに,記録媒体から遠い側では同極同士の反発力 を受ける(かつてはこれがマグネトグラフィで濃い画面 を実現することの難しさであるといわれていた¹)。こ のようにマグネトグラフィでは磁性トナーが常にN,S両極を持った双極子として存在するが,このことは電子写真や静電記録におけるトナーが+またはーの電荷を持 つ単極粒子として存在するのと本質的に異なる点であ る。
Retry
Reason
2.2 記録媒体から磁性トナーに働く磁気力 Retry Reason
ここで


Fig. 1 記録媒体の磁荷とトナーに誘導される磁荷の関係。
Retry
Reason
NRZ(Non-Return to Zero)記録を行ったときの転移領域を逆正接関数近似すると,磁界と磁気力は以下の近似式で表される
(磁荷の正負と複合同順)
Retry
Reason
までの距離 Retry Reason
これらの式から点
Fig. 2 に磁気力の分布を,Fig. 3 に磁界と磁気力の分布のベクトル表示を示す。
Fig. 2 より
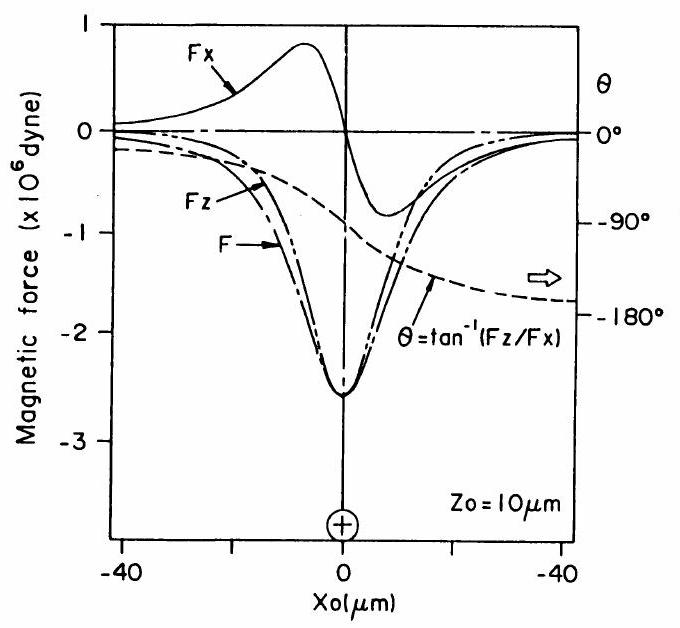
Fig. 2 より

Fig. 3 記録媒体から生ずる磁界と磁気力のベクトル表示.
Retry
Reason
(a)磁界分布のベクトル表示 Retry Reason
(b)磁気力分布のベクトル表示 Retry Reason
(c)記録媒体内の磁化パターン Retry Reason
(a)磁界分布のベクトル表示 Retry Reason
(b)磁気力分布のベクトル表示 Retry Reason
(c)記録媒体内の磁化パターン Retry Reason
大になる。これは磁化転移領域から外に出て行こうとす るトナーを転移領域内に引き込もうとする力が,最も強 く働くことを意味する。磁荷中心
Fig. 3 において磁界のベクトルが仮想磁荷中心から外に向いているのに対して,磁気力のベクトルの矢は仮想磁荷中心
Fig. 3 において磁界のベクトルが仮想磁荷中心から外に向いているのに対して,磁気力のベクトルの矢は仮想磁荷中心
磁気力の大きさは
3.現 像 Retry Reason
電子写真の現像法はトナーが(+)または( — )という電荷を帯びた単極粒子として振舞うことを利用している が、マグネトグラフィでは 1 個のトナーの中に N,S両極があって,双極子として振る舞うため,新しい現像法の開発が必要であった。ここでは筆者らが開発した, トナーが双極子であるという性質に適合した弱磁界現像法(磁気チェーン法)を紹介する
3.1 弱磁界現像法(磁気チェーン法)の原理 Retry Reason
現像プロセスは現像機から記録媒体へのトナーの引渡 しのプロセスである.Fig. 4 に弱磁界現像法の原理を示 す.(a)に示すようにトナーを現像磁界により磁化して
Retry
Reason
(a) Retry Reason

(b) Retry Reason

(a) Retry Reason

(b) Retry Reason

Fig. 4 弱磁界(磁気チェーン)現像法の原理。 (a)現像前(b)現像後
Retry
Reason
チェーン状に連ねておく。記録媒体の転移領域からは空中に潜像磁界が生じている。記録媒体のトナー吸引力と現像磁界との関係が次の条件を満たすように設定する。
Retry
Reason
画像部:記録媒体のトナー吸引力>トナーチェーンの結合力
Retry
Reason
非画像部:記録媒体のトナー吸引力<トナーチェーン の結合力 Retry Reason
(b)に示すようにこの状態で記録媒体とトナーとを接触させると,記録媒体の画像部は媒体磁荷から近いため磁気吸引力が強く,かつ潜像磁界と現像磁界の向きとが同じであるから,トナーはそのままの向きですんなりと記録媒体側に移動し,黒画像を形成する。他方,記録媒体の背景部では潜像磁界と現像磁界の向きが逆であるた め、トナーを移動させるにはトナーの磁化の向きを逆転 させなければならない。が,この部分は媒体磁荷から遠 いため潜像磁界が弱いので、トナーはチェーン状のまま現像磁界側にとどまり,記録媒体側に移ってこない。こ うして画像部にトナーを引き渡し,背景部にトナーが付着するのを防止することができる。 Retry Reason
非画像部:記録媒体のトナー吸引力<トナーチェーン の結合力 Retry Reason
(b)に示すようにこの状態で記録媒体とトナーとを接触させると,記録媒体の画像部は媒体磁荷から近いため磁気吸引力が強く,かつ潜像磁界と現像磁界の向きとが同じであるから,トナーはそのままの向きですんなりと記録媒体側に移動し,黒画像を形成する。他方,記録媒体の背景部では潜像磁界と現像磁界の向きが逆であるた め、トナーを移動させるにはトナーの磁化の向きを逆転 させなければならない。が,この部分は媒体磁荷から遠 いため潜像磁界が弱いので、トナーはチェーン状のまま現像磁界側にとどまり,記録媒体側に移ってこない。こ うして画像部にトナーを引き渡し,背景部にトナーが付着するのを防止することができる。 Retry Reason
3.2 現像機の構成 Retry Reason
Fig. 5 に基本的な現像機の構造と記録ドラムとの配置関係を示す。現像ロールは回転する非磁性のスリーブ と,それに囲まれて固定された磁気ロールとからなる。磁気ロールの
3.3 現像磁界の強さ Retry Reason
Fig. 5 現像機の基本構成と配置。
Retry
Reason
- *明星大学,理工学部電気工学科
〒191 東京都日野市程久保 2-1-1 Retry Reason
*Electrical Engineering Department,Faculty of Science and Engineering,Meisei University Retry Reason
2-1-1 Hodokubo Hino-shi,Tokyo, 191 Japan Retry Reason


